各水模型比较
本文收集了50种水模型,按粒子数/极化、时间进行分类,对比各自的特点、参数、性能。
三点水模型: H-O-H
SPC: 冰四面体几何结构
- SPC/E: SPC考虑有效成对(pair)相互作用
- SPC/Eb: 改善平移、旋转扩散系数
- SPC/Fd: 考虑分子柔性,即键O-H/H-H伸缩、角H-O-H转动势能
- SPC/Fw: 考虑分子柔性,即键O-H伸缩、角H-O-H转动势能;键长键角不同于SPC
- SPC/ε: 改善介电常数
TIP3P: 气相水几何结构
- TIP3P/Fw: 考虑质子传输,被视为考虑了水分子柔性,部分文章称其为TIP3P/Fs
- TIP3P-Ew: 优化静电相互作用的Ewald求和方法
- TIP3P-FB: 类似于机器学习,通过最终的性质(液体、多个冰相、从头算)优化分子的结构参数,FB为ForceBalance
- TIP3P-ST: 与FB同源,加入了液体表面张力(Surface Tension),
- TIPS3P: 考虑H的范德华相互作用(如无特殊说明,模型均未考虑)
其他系列
- CVFF: 是一套力场参数,其中水模型几何结构与TIP3P相近,LJ参数与SPC相近,柔性略小于SPC/Fw和TIP3P/Fw,注意,其力场中对HW使用了更小的半径
- CVFF(cm): CVFF的改进版,对O-H引入交叉项和Morse势能
- PCFF: 是一套力场参数,其中水模型几何结构与TIP3P相近,O的LJ项变化较大(相较于SPC、TIP3P),引入了H的LJ项
- COMPASS:是一套力场参数,其中水模型几何结构与TIP3P相近,O的LJ项变化较大,引入了H的LJ项
- FBA/ε: Flexible Bond and Angle,柔性键角模型,各结构参数变化较大;改善介电常数
- H2O-DC: 优化介电常数,其结构更接近TIP3P,但作者并没有命名为TIP3P-DC
- SPC/DC: 优化介电常数,其结构更接近SPC
- F3C: Flexible 3-Centered,引入H的LJ项
- OPC3: 3-point Optimal Point Charge,OPC的三点模型,移除了虚拟位点,参考OPC;从参数值上看,与SPC/ε差不多
四点水模型: H-O(M)-H
TIP4P
- TIP4P: 在三点水模型中,将O的负电荷M分离出来,放置在分子质心,且电荷数值不同于TIP3P;优化了结构性质
- TIP4P-Ew: 优化静电相互作用的Ewald求和方法
- TIP4P/2005: TIP4P重参数化,拟合更宽温度、压力范围的性质数值
- TIP4P/Ice:专门优化了冰的性质,但其他性质并没有恶化
- TIP4P/2005f: 在TIP4P/2005基础上考虑了柔性,且使用Morse势能描述O-H键
- TIP4P-D: 优化色散相互作用(即C12项)
- TIP4P-FB: FB系列
- TIP4P-ST: ST系列
- TIP4P/ε: 优化介电常数
OPC
- OPC: 优化点电荷分布;被视为最优四点模型
多点水模型
- TIP5P: H-O(L)(L)-H,在三点水模型上,在O附近加入两个孤对电子L;复现-37~100 ℃、1~10000 atm水的密度
- TIP5P-Ew: 优化静电相互作用的Ewald求和方法
- TIP5P-2018: 改善等温压缩性
- TIP6P: H-O(M)(L)(L)-H,在TIP5P上保留TIP4P的M
- TIP7P: H-O(M)(M)(L)(L)-H,在TIP6P的基础上,将M分裂为两个,M位于O-H的中心
可极化水模型
古董
- PD: polarizable point dipole,在每个可极化中心上放置一个感应点偶极子
- FQ: fluctuating charge (fluc-q),原子位点上的点电荷可以响应环境而波动;SPC-FQ、TIP4P-FQ
- DO: Drude oscillator,结合PD和FQ,使用谐波抑制势能函数将固定大小的移动点电荷拴在特定的相互作用位点
COS
-
STR/1: 感应偶极矩由一对固定大小的分离电荷表示;四个位点,H-O(pol)-H, O与H电荷平衡,O带电不为qO,而是qO-qpol,qpol为极化电荷位点带电量=-8
-
COS/G: 永久偶极矩与气相水偶极矩相当
-
COS/B1、COS/B2: 更大的永久偶极矩
-
COS/G2: 五位点,H-O(M-pol)-H,O不带电,转移到M点,M与H电荷平衡,qpol=-8
-
COS/G3: O-M距离更小
-
COS/D: 引入了两个新参数p、E0来定义极化率的阻尼
-
COS/D2: COS/D的优化版,兼容生物分子力场GROMOS,且增加了H-H的排斥力
其他
- SWM4-DP: Drude极性简单水模型,引入Drude位点,对D-O引入Drude谐振子,使氧负电荷可移动;注意M与H电荷平衡,D与M重合并额外带电与O平衡;O带负电
- SWM4-NDP: 同SWM4-DP,O带正电
- SWM6: 在TIP6P中O上引入Drude谐振子
- ABEEM-7P: 将DFT的Electronegativity Equalization引入到分子动力学中;H-O(M)(M)(L)(L)-H,位点按O H的半径比例决定
- OPC3-pol: OPC3的可极化模型,M和O都带电荷,增加了M与O的力常数;允许4fs步长MD
时间发展图
| 三点 | 四点 | 多点 | 可极化 | ||||
|---|---|---|---|---|---|---|---|
| 1981 | SPC | ||||||
| 1983 | TIP3P | TIP4P | |||||
| 1985 | TIPS3P | ||||||
| 1987 | SPC/E | ||||||
| SPC/Fd | |||||||
| 1988 | CVFF*, CVFF(cm)* |
||||||
| 1990 | STR/1 | ||||||
| 1994 | PCFF* | SPC-FQ, TIP4P-FQ |
|||||
| 1997 | F3C | ||||||
| 1998 | COMPASS* | ||||||
| TIP3P-Fw | |||||||
| 2000 | TIP5P | ||||||
| 2003 | TIP6P | SWM4-DP | COS/G, COS/B1, COS/B2 |
||||
| 2004 | TIP3P-Ew | TIP4P-Ew | TIP5P-Ew | ABEEM-7P | COS/G2, COS/G3 |
||
| 2005 | TIP4P/2005 | ||||||
| TIP4P/Ice | |||||||
| 2006 | SPC/Fw | SWM4-NDP | |||||
| 2009 | COS/D | ||||||
| 2011 | TIP4P/2005f | ||||||
| 2012 | SPC/DC | H2O-DC | |||||
| 2013 | SWM6 | ||||||
| 2014 | TIP3P-FB | TIP4P-FB | COS/D2 | ||||
| TIP4P/ε | |||||||
| OPC | |||||||
| 2015 | SPC/ε | TIP4P-D | |||||
| 2016 | OPC3 | ||||||
| 2018 | TIP5P-2018 | ||||||
| 2019 | TIPSP-ST | TIP4P-ST | TIP7P | ||||
| 2020 | FBA/ε | ||||||
| 2022 | OPC-pol | ||||||
| . . . |
|||||||
部分性能测试
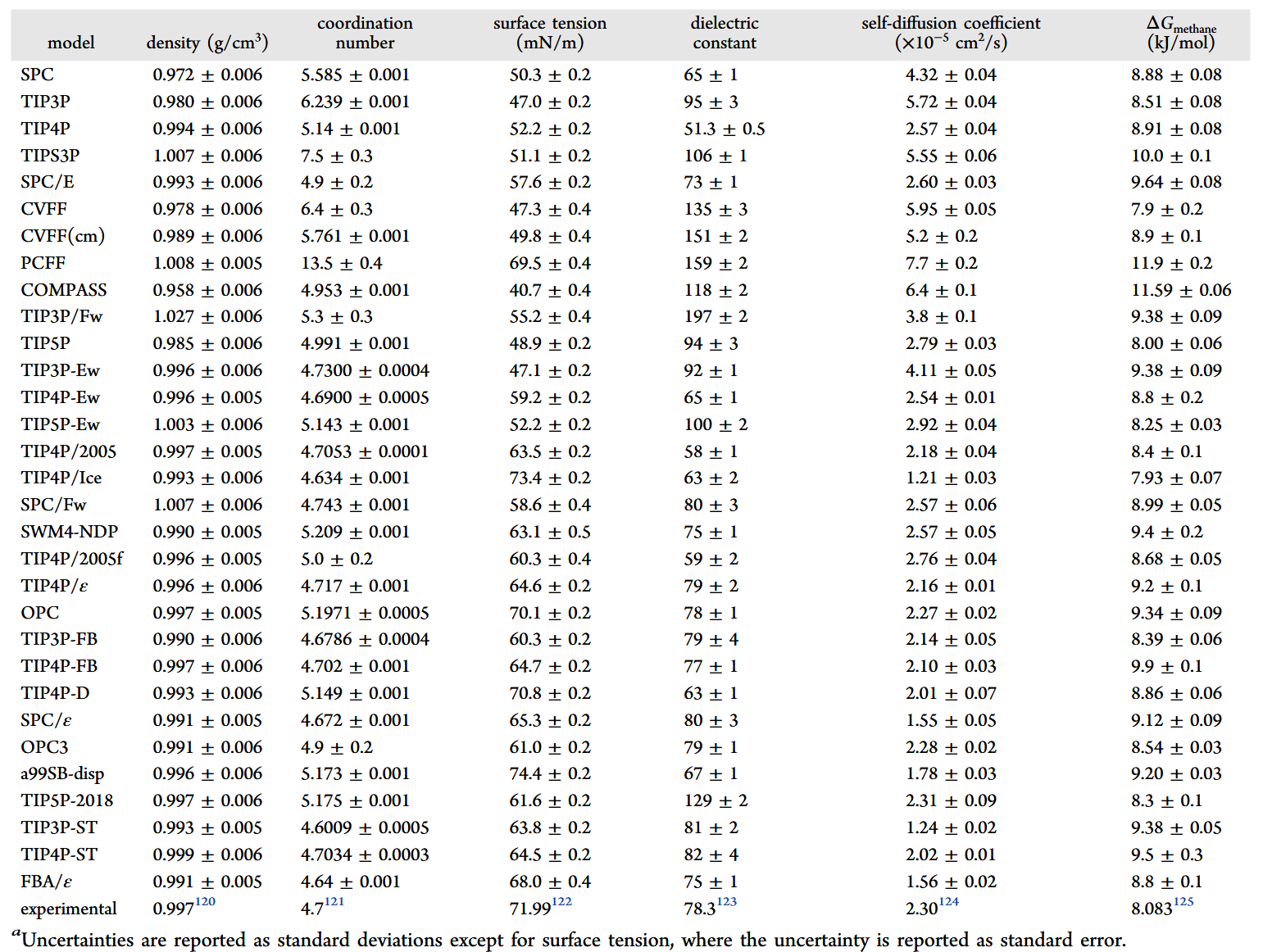
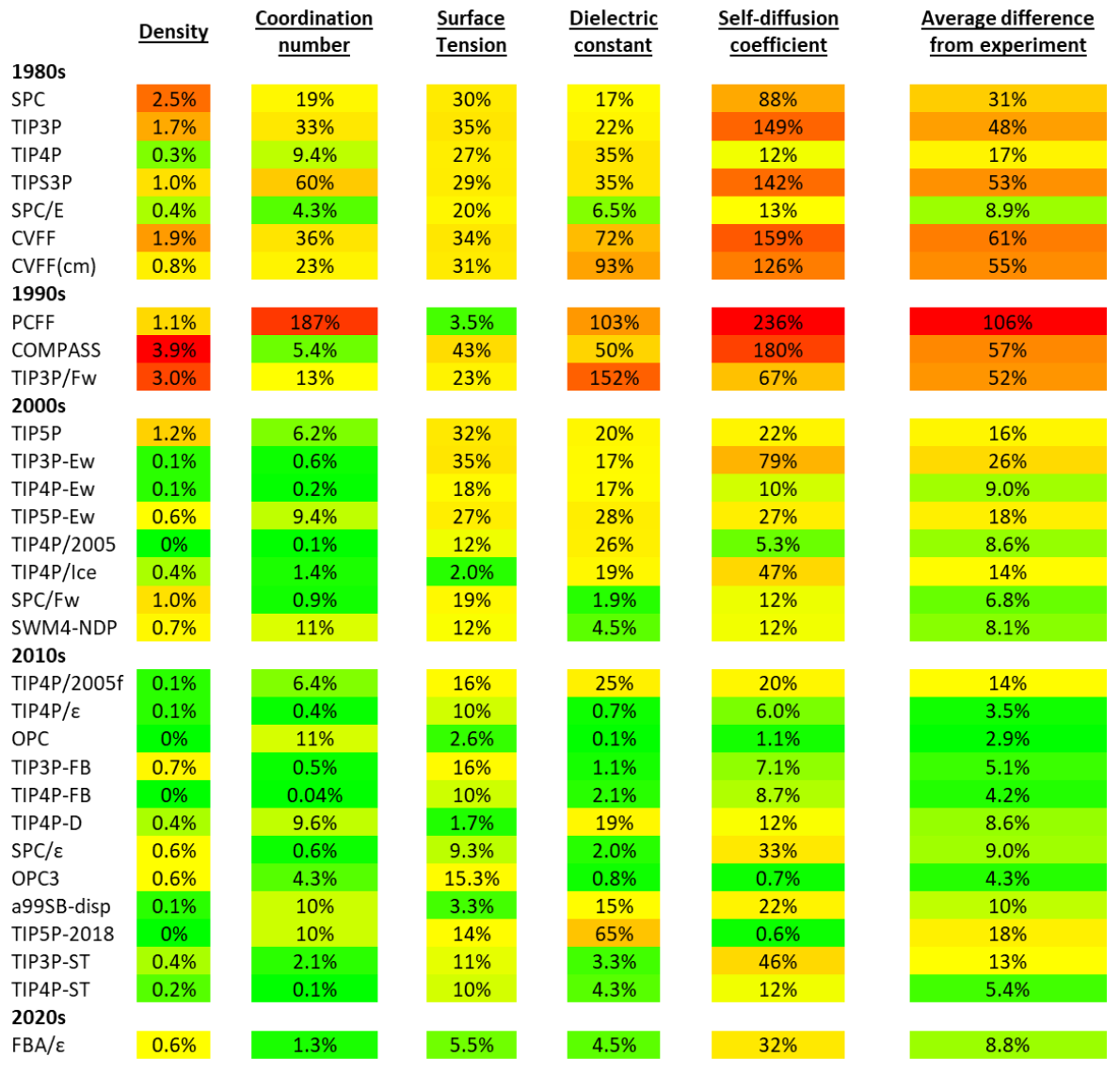
更多性质参考 Water Structure and Science ,上次更新为2022年,部分新模型未加入,如opc-pol、ST系列
参数表
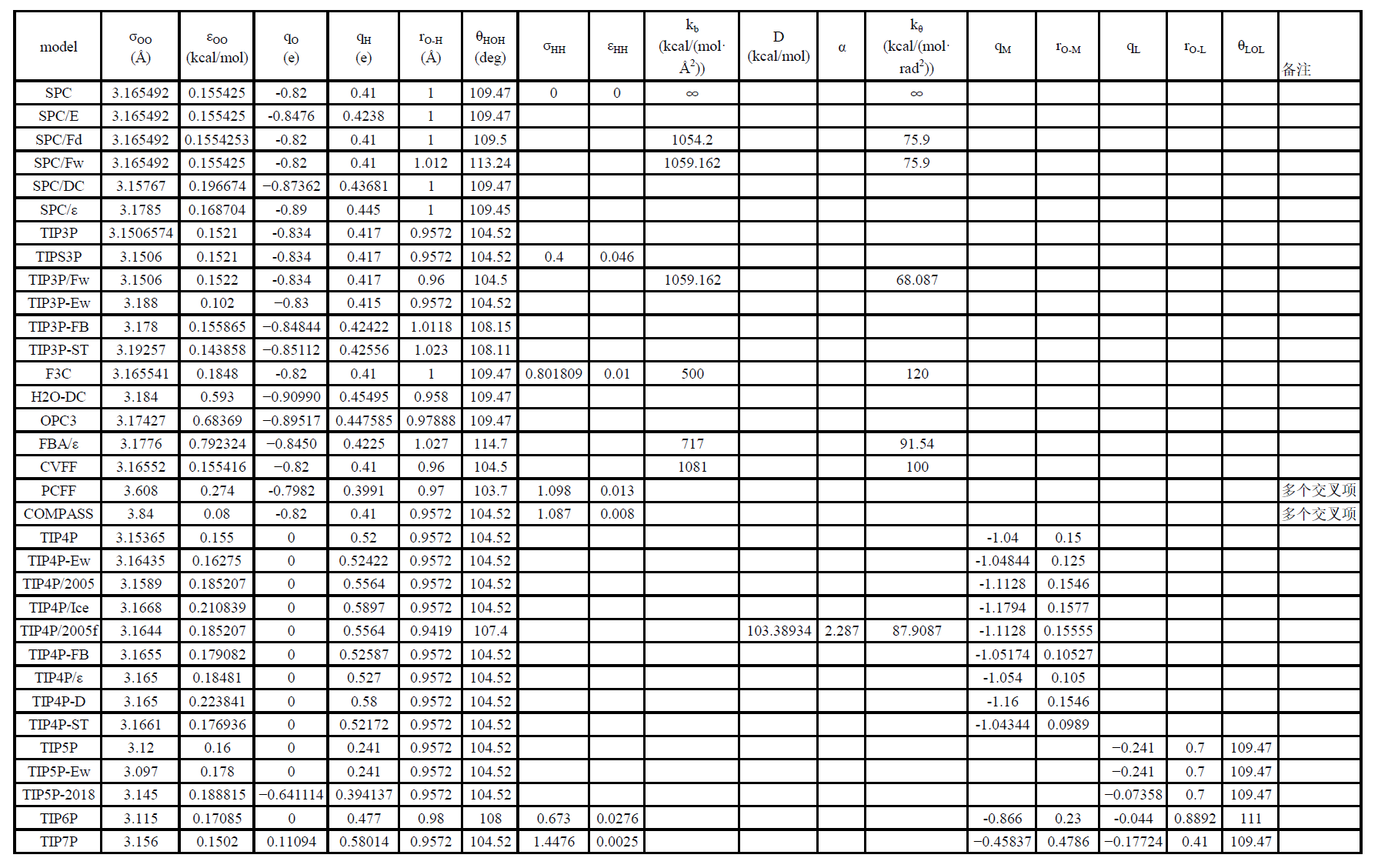
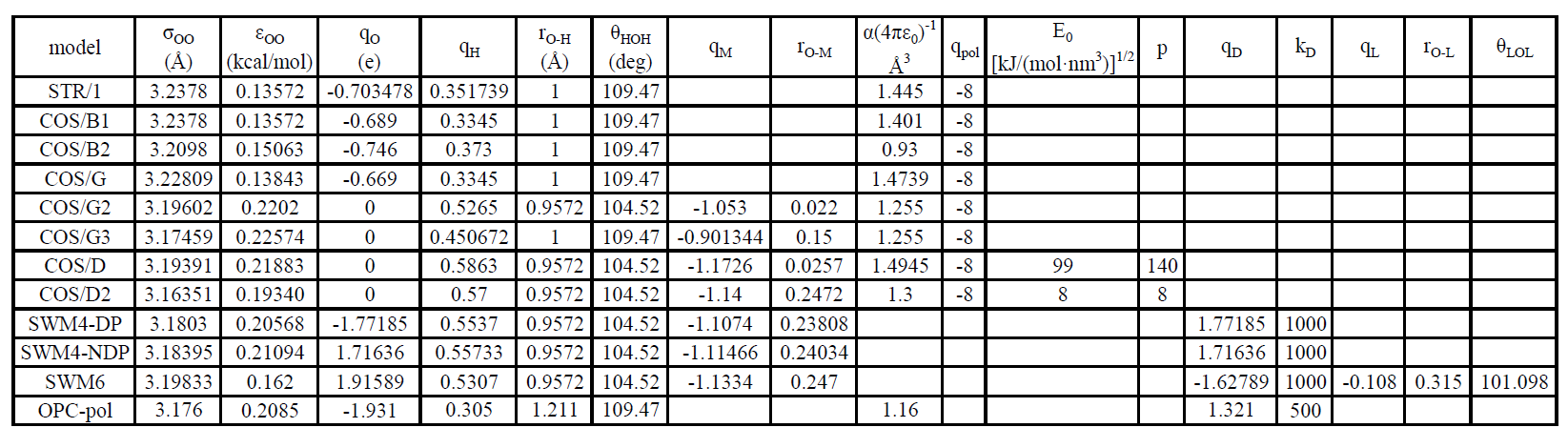
- FQ系列力场形式大不相同,故不列出对比
- 图中所有力常数kb、kθ均为1/2*k*()2形式中的参数,部分原文献使用Kb、Kθ为K*()2形式的参数,且部分文献对比常数k时引用的是K,如Wu Y, Tepper H L, Voth G A. Flexible simple point-charge water model with improved liquid-state properties[J]. The Journal of Chemical Physics, 2006, 124(2)[2025-07-15].引用F3C错误,故需注意。
- 此外,部分远古论文找不到原文献,或者是商业力场,参数来源于二次引用论文;引用过程中可能出现有效数字不同;单位换算导致数值不同,如σ和Rmin、σε和AB或C12 C6
参考文献
[1]
Mahoney M W, Jorgensen W L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions[J]. The Journal of Chemical Physics, 2000, 112(20): 8910-8922.
[2]
González M A, Abascal J L F. A flexible model for water based on TIP4P/2005[J]. The Journal of Chemical Physics, 2011, 135(22)[2025-07-16].
[3]
Abascal J L F, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005[J]. The Journal of Chemical Physics, 2005, 123(23)[2025-07-16].
[4]
Price D J, Brooks C L III. A modified TIP3P water potential for simulation with ewald summation[J]. The Journal of Chemical Physics, 2004, 121(20): 10096-10103.
[5]
Lamoureux G, Harder E, Vorobyov I V, et al. A polarizable model of water for molecular dynamics simulations of biomolecules[J]. Chemical Physics Letters, 2006, 418(1): 245-249.
[6]
Abascal J L F, Sanz E, García Fernández R, et al. A potential model for the study of ices and amorphous water: TIP4P/ice[J]. The Journal of Chemical Physics, 2005, 122(23)[2025-07-16].
[7]
Rick S W. A reoptimization of the five-site water potential (TIP5P) for use with ewald sums[J]. The Journal of Chemical Physics, 2004, 120(13): 6085-6093.
[8]
Lamoureux G, MacKerell A D, Roux B. A simple polarizable model of water based on classical drude oscillators[J]. The Journal of Chemical Physics, 2003, 119(10): 5185-5197.
[9]
Yu H, van Gunsteren W F. Accounting for polarization in molecular simulation[J]. Computer Physics Communications, 2005, 172(2): 69-85.
[10]
Izadi S, Onufriev A V. Accuracy limit of rigid 3-point water models[J]. The Journal of Chemical Physics, 2016, 145(7): 074501.
[11]
Bachmann S J, Van Gunsteren W F. An improved simple polarisable water model for use in biomolecular simulation[J]. The Journal of Chemical Physics, 2014, 141(22)[2025-07-17].
[12]
Nada H, Van Der Eerden J P J M. An intermolecular potential model for the simulation of ice and water near the melting point: A six-site model of H2O[J]. The Journal of Chemical Physics, 2003, 118(16): 7401-7413.
[13]
Yang Z Z, Wu Y, Zhao D X. Atom-bond electronegativity equalization method fused into molecular mechanics. I. A seven-site fluctuating charge and flexible body water potential function for water clusters[J]. The Journal of Chemical Physics, 2004, 120(6): 2541-2557.
[14]
Wang L P, Martinez T J, Pande V S. Building force fields: An automatic, systematic, and reproducible approach[J]. The Journal of Physical Chemistry Letters, 2014, 5(11): 1885-1891.
[15]
Izadi S, Anandakrishnan R, Onufriev A V. Building water models: A different approach[J]. The Journal of Physical Chemistry Letters, 2014, 5(21): 3863-3871.
[16]
Levitt M, Hirshberg M, Sharon R, et al. Calibration and testing of a water model for simulation of the molecular dynamics of proteins and nucleic acids in solution[J]. The Journal of Physical Chemistry B, 1997, 101(25): 5051-5061.
[17]
Yu H, Van Gunsteren W F. Charge-on-spring polarizable water models revisited: From water clusters to liquid water to ice[J]. The Journal of Chemical Physics, 2004, 121(19): 9549-9564.
[18]
Jorgensen W L, Chandrasekhar J, Madura J D, et al. Comparison of simple potential functions for simulating liquid water[J]. The Journal of Chemical Physics, 1983, 79(2): 926-935.
[19]
Kunz A P E, Van Gunsteren W F. Development of a nonlinear classical polarization model for liquid water and aqueous solutions: COS/D[J]. The Journal of Physical Chemistry A, 2009, 113(43): 11570-11579.
[20]
Yu H, Hansson T, Van Gunsteren W F. Development of a simple, self-consistent polarizable model for liquid water[J]. The Journal of Chemical Physics, 2003, 118(1): 221-234.
[21]
Horn H W, Swope W C, Pitera J W, et al. Development of an improved four-site water model for biomolecular simulations: TIP4P-ew[J]. The Journal of Chemical Physics, 2004, 120(20): 9665-9678.
[22]
Rick S W, Stuart S J, Berne B J. Dynamical fluctuating charge force fields: Application to liquid water[J]. The Journal of Chemical Physics, 1994, 101(7): 6141-6156.
[23]
Xiong Y, Izadi S, Onufriev A V. Fast polarizable water model for atomistic simulations[J]. Journal of Chemical Theory and Computation, 2022, 18(10): 6324-6333.
[24]
Fuentes-Azcatl R, Barbosa M C. Flexible bond and angle, FBA/ϵ model of water[J]. Journal of Molecular Liquids, 2020, 303: 112598.
[25]
Wu Y, Tepper H L, Voth G A. Flexible simple point-charge water model with improved liquid-state properties[J]. The Journal of Chemical Physics, 2006, 124(2)[2025-07-15].
[26]
Khalak Y, Baumeier B, Karttunen M. Improved general-purpose five-point model for water: TIP5P/2018[J]. The Journal of Chemical Physics, 2018, 149(22).
[27]
Fuentes-Azcatl R, Mendoza N, Alejandre J. Improved SPC force field of water based on the dielectric constant: SPC/ε<math><mi is="true">ε</mi></math>[J]. Physica A: Statistical Mechanics and its Applications, 2015, 420: 116-123.
[28]
H.J.C.Ber endsen. Interaction models for water in relation to protein hydration | SpringerLink[J]. Springer Nature Link, 1981[2025-07-15].
[29]
Straatsma T P, McCammon J A. Molecular Dynamics Simulations with Interaction Potentials Including Polarization Development of a Noniterative Method and Application to Water[J]. Molecular Simulation, 1990, 5(3-4): 181-192.
[30]
Zhao D, Huang Y, Shen H. Neural network-based molecular dynamics simulation of water assisted by active learning[J]. The Journal of Physical Chemistry B, 2025, 129(15): 3829-3838.
[31]
Fuentes-Azcatl R, Alejandre J. Non-polarizable force field of water based on the dielectric constant: TIP4P/ε[J]. The Journal of Physical Chemistry B, 2014, 118(5): 1263-1272.
[32]
Vega C, Abascal J L F. Relation between the melting temperature and the temperature of maximum density for the most common models of water[J]. The Journal of Chemical Physics, 2005, 123(14)[2025-07-16].
[33]
Zhao C L, Zhao D X, Bei C C, et al. Seven-site effective pair potential for simulating liquid water[J]. The Journal of Physical Chemistry B, 2019, 123(21): 4594-4603.
[34]
Dang L X, Pettitt B Montgomery. Simple intramolecular model potentials for water[J]. The Journal of Physical Chemistry, 1987, 91(12): 3349-3354.
[35]
Fennell C J, Li L, Dill K A. Simple liquid models with corrected dielectric constants[J]. The Journal of Physical Chemistry B, 2012, 116(23): 6936-6944.
[36]
Yu W, Lopes P E M, Roux B, et al. Six-site polarizable model of water based on the classical drude oscillator[J]. The Journal of Chemical Physics, 2013, 138(3)[2025-07-17].
[37]
Kadaoluwa Pathirannahalage S P, Meftahi N, Elbourne A, et al. Systematic comparison of the structural and dynamic properties of commonly used water models for molecular dynamics simulations[J]. Journal of Chemical Information and Modeling, 2021, 61(9): 4521-4536.
[38]
Qiu Y, Nerenberg P S, Head-Gordon T, et al. Systematic Optimization of Water Models Using Liquid/Vapor Surface Tension Data[J]. The Journal of Physical Chemistry B, 2019, 123(32): 7061-7073.
[39]
Schmitt U W, Voth G A. The computer simulation of proton transport in water[J]. The Journal of Chemical Physics, 1999, 111(20): 9361-9381.
[40]
Berendsen H J C, Grigera J R, Straatsma T P. The missing term in effective pair potentials[J]. The Journal of Physical Chemistry, 1987, 91(24): 6269-6271.
[41]
Piana S, Donchev A G, Robustelli P, et al. Water dispersion interactions strongly influence simulated structural properties of disordered protein states[J]. The Journal of Physical Chemistry B, 2015, 119(16): 5113-5123.
[42]
Takemura K, Kitao A. Water model tuning for improved reproduction of rotational diffusion and NMR spectral density[J]. The Journal of Physical Chemistry B, 2012, 116(22): 6279-6287.
[43]
Water models[EB]. (2022)[2025-07-15].
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 星星点灯!